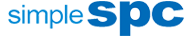More Powerful. More Efficient. Built for Complex Quality Scenarios.

Following its recognition as a Recommended SPC Software in 2025, Bingo SPC is proud to announce the official release of SPC 4.0 in early 2026.

This major upgrade represents a significant leap forward—not only in statistical rigor, but also in operational efficiency, system scalability, and enterprise-grade usability. SPC 4.0 is designed to support more complex manufacturing scenarios while delivering faster insights and stronger process control.

1. Statistical Core: Built for Complex and Real-World Scenarios

Key focus: Breaking the limitations of fixed data structures

• Support for Variable Subgroup Sizes
  SPC 4.0 fully supports non-fixed subgroup data. All SPC reports, control chart algorithms, and monitoring modules have been upgraded accordingly, effectively addressing real-world sampling variability in production environments.
• Expanded Control Chart Algorithms
  New control charts, including MR-R/S Mean Charts and Moving Range Mean Charts, have been introduced to enhance statistical analysis for small samples and variable subgroups.
• Text-Based Data Traceability
  A new Text Data Type (Type 8) has been added, enabling the recording, upload, and traceability of non-numerical quality information—extending SPC coverage beyond purely quantitative data.

2. Analytical Tools: From Single Calculations to Advanced Diagnostics

Key focus: A productivity multiplier for Quality Engineers

• Enhanced CPK “All-in-One” Analysis
  The CPK analysis tool has been fully redesigned into a six-in-one diagnostic report, generating control charts, normal probability plots, capability comparison charts, histograms, and run charts in a single execution.
• Simulation and Capability Forecasting
  Users can now generate simulated datasets based on target CPK values, supporting process capability estimation and scenario analysis.
• Interactive Statistical Analysis
  Regression analysis, ANOVA, and t-tests now leverage interactive, spreadsheet-style interfaces, allowing samples to be selected directly from raw data for near-instant analysis.
• Optimized Visualization Performance
  Box plots, distribution fitting, and related charts now support significantly larger datasets with improved rendering performance and additional reference line options.

3. Monitoring and Alerts: From Detection to Closed-Loop Control

Key focus: Turning signals into actions

• Alert Frequency Optimization
  A new minimum alert interval prevents notification overload in high-frequency data environments. Historical alerts retain the corresponding specification limits and capability indices at the time of triggering.
• Multi-Dimensional Alert Strategies
  Alerts can now be triggered based on SPC out-of-control signals or insufficient CPK/PPK capability, with flexible recipient grouping and retry mechanisms.
• Closed-Loop Exception Management
  Improvement actions are deeply linked to abnormal events, with support for response rate statistics and logical deletion of resolved abnormal points—strengthening end-to-end quality issue closure.

4. Dashboards & Visualization: Multi-Dimensional Insights

Key focus: Clear visibility for informed decisions

• Statistical Dashboard (New Module)
  A dedicated management-level dashboard provides a comprehensive overview of SPC operations across the organization. Highly flexible chart definitions can be created using custom SQL, enabling enterprise-wide monitoring.
• Dynamic and Composite Dashboards
  Dashboards support automatic and manual switching modes, merged page displays, and configurable page dwell times. Dashboard categories and role-based access control are fully supported.

5. Data Entry & Collection: Seamless Multi-Device Collaboration

Key focus: Real-time accuracy and efficiency

• Multi-Platform Data Entry
  A new mobile data entry interface has been introduced. Manual entry screens now provide real-time feedback on process capability indicators (CPK/PPK).
• Full Data-Type Coverage
  Enhanced support for descriptive inspection items and variable subgroup inspection data.
• Advanced Automated Data Collection
  New JSON-based data acquisition configurations and direct synchronization with SAP inspection plans are supported.
• Measurement Device Integration
  Web serial port technology enables direct acquisition of data from electronic gauges and measuring instruments, automatically populating data entry forms.

6. System Foundation: Performance, Stability, and Security

Key focus: Faster, stronger, and more secure

• Performance Enhancements
  Bulk Excel data uploads are now up to 10× faster. Database connection pool optimization eliminates interface freezing under high-concurrency conditions.
• Global Time Zone Support
  User-level time zone configuration ensures accurate timestamp handling across global and multi-site deployments.
• Built-in System Maintenance
  Integrated log cleanup, monitoring image management, and SFTP-based remote data backup simplify system maintenance.
• Granular Access Control
  Fine-grained authorization for dashboards and pages by category, with global administrative override support for Admin accounts.

SPC 4.0 Is Ready

SPC 4.0 is now fully available.
We recommend starting with the enhanced CPK six-in-one analysis report and the new Statistical Dashboard to experience the most significant improvements firsthand.

I. Pharmaceutical Manufacturing: Why Process Stability Matters

In the pharmaceutical industry, the consequences of quality issues extend far beyond economic loss. They directly affect patient safety and expose companies to significant regulatory and compliance risks.

Compared with other manufacturing sectors, pharmaceutical production has several defining characteristics:

• Highly complex processes with numerous variables

• Extremely stringent quality requirements with minimal allowable variability

• Any abnormality may result in batch rejection, production shutdowns, or product recalls

• Strict regulatory oversight under frameworks such as GMP and authorities including the NMPA, FDA, and EMA

As a result, the core challenge of pharmaceutical quality management is not simply whether a product meets specifications, but whether:

The manufacturing process remains consistently controlled, stable, and predictable.

This is precisely where Statistical Process Control (SPC) delivers its fundamental value in the pharmaceutical industry.

II. The Role of SPC in Pharmaceutical Manufacturing

In pharmaceutical manufacturing, SPC is far more than a basic statistical quality tool. It serves as:

• A critical method for maintaining continuous process control

• A key data foundation within GMP systems

• A vital bridge connecting processes, equipment, quality, and regulatory compliance

By continuously monitoring Critical Process Parameters (CPPs) and Critical Quality Attributes (CQAs), SPC enables pharmaceutical companies to:

• Detect abnormal trends at an early stage

• Prevent deviations from escalating into quality incidents

• Provide objective, data-driven evidence for deviation investigations and CAPA activities

III. Typical Application Scenarios of SPC in Pharmaceutical Manufacturing

1. Raw Materials and Pre-processing

In active pharmaceutical ingredient (API) and finished dosage manufacturing, SPC is commonly applied to monitor:

• Key physicochemical attributes of raw and excipient materials

• Particle size distribution and moisture content

• Weighing accuracy and variability

SPC allows early identification of abnormal fluctuations in raw materials or pre-processing steps, preventing issues from propagating downstream into subsequent processes.

2. Finished Dosage Manufacturing Process Control

In solid and liquid dosage form manufacturing, SPC is widely used to monitor:

• Mixing time and blend uniformity

• Tablet weight, hardness, and thickness

• Fill volume accuracy and sealing quality

SPC helps distinguish between:

• Random variation, and

• Systematic shifts or equipment-related abnormalities,

thereby reducing batch-to-batch variability and ensuring consistent product quality.

3. Aseptic and Cleanroom-Related Processes

For sterile products and biopharmaceutical manufacturing, SPC plays a particularly critical role in monitoring:

• Environmental conditions (temperature, humidity, microbial levels, particle counts)

• Sterilization process parameters

• Operating status of critical equipment

Trend-based control charts enable early detection of potential loss-of-control conditions, helping prevent sterility failures before they occur.

4. Packaging and Labeling Processes

During the packaging stage, SPC is commonly applied to:

• Fill consistency

• Seal integrity

• Label positioning and readability

Effective process control at this stage significantly reduces compliance risks related to mislabeling, underfilling, or packaging defects.

IV. Key Characteristics of SPC in the Pharmaceutical Industry

1. Strong Compliance Orientation

SPC data is frequently used to support:

• GMP audits and inspections

• Deviation investigations

• Verification of CAPA effectiveness

By translating abstract GMP requirements into measurable and continuously monitored process indicators, SPC plays a critical role across all quality assurance activities. Data integrity, traceability, and audit readiness are especially essential.

2. Greater Focus on Trends Rather Than Single Limit Exceedances

In pharmaceutical manufacturing, many quality risks do not arise from isolated out-of-specification events, but from:

Gradual and long-term process drift.

SPC trend analysis enables proactive intervention before deviations formally occur.

3. Integration with Validation and Continued Process Verification

SPC is often implemented in conjunction with:

• Process Validation (PV)

• Continued Process Verification (CPV)

forming a core component of lifecycle process management.

V. Core Value Delivered by SPC to Pharmaceutical Companies

• Improved process stability and product consistency

• Reduced risk of batch deviations and product rejection

• Stronger support for GMP compliance and regulatory audits

• More efficient deviation handling and CAPA execution

• Establishment of a data-driven quality culture

As regulatory expectations continue to increase, SPC has evolved from an optional tool into a foundational capability within pharmaceutical quality systems.

VI. Conclusion: SPC as the “Second Line of Defense” in Pharmaceutical Quality

In the pharmaceutical industry:

Compliance is the baseline. Stability is the core. Data is the safeguard.

Through continuous monitoring and trend analysis, SPC enables manufacturers to take action before problems occur—protecting patient safety, reducing operational risk, and supporting long-term, stable production.

Truly mature pharmaceutical manufacturing does not rely on end-product testing alone, but on controlled and predictable processes.

The automotive industry is characterized by a large number of parts, complex processes, and extremely high quality requirements. A complete vehicle often consists of tens of thousands of parts, involving stamping, welding, painting, final assembly, and the production of numerous outsourced parts. Fluctuations in any stage can be amplified into batch quality problems, leading to high risks of rework, claims, and even recalls.

SPC (Statistical Process Control) is a quality management method developed to address the issues of process stability, controllable fluctuations, and early detection of anomalies. It is not a post-event inspection but a process prevention management tool, which aligns perfectly with the automotive industry's pursuit of "zero defects" and "continuous improvement."

II. Typical Application Scenarios of SPC in the Automotive Industry

1. Stamping Process: Dimensional Stability Control

Common critical quality characteristics (CTQs) in the stamping process include:

* Sheet length, width, hole dimensions
* Flatness, warpage
* Burr height

Through Xbar-R control charts / Xbar-S control charts, it is possible to:

* Monitor die wear trends in real time
* Detect equipment anomalies early
* Avoid batch defects caused by dimensional drift

Typical benefits:

* Reduce unplanned die downtime
* Extend die life
* Reduce first and final inspection pressure

2. Welding Process: Process Consistency Monitoring

Key indicators in the welding process include:

* Weld strength
* Weld position deviation
* Number of welds

SPC can be combined with:

* Measurement control charts (Xbar-R): Weld pull-out force
* Count control charts (P-chart / U-chart): Welding defect rate

Typical benefits:

* Identify welding torch wear and current fluctuations
* Prevent structural strength defects
* Meet OEM audit requirements (e.g., VDA, IATF 16949)

3. Painting Process: Dual Control of Appearance and Performance

Painting is one of the most "sensitive" processes in automotive quality. SPC is commonly used to monitor:

  *  Film thickness
  *  Gloss
  *  Color difference (ΔE)
  *  Defect rates such as particles and runs

SPC can help:

  *  Monitor changes in painting equipment and environment
  *  Analyze the impact of temperature and humidity on painting quality
  *  Reduce repainting and repair costs

4. Final Assembly and Component Assembly: Preventing Systemic Defects

In final assembly and component assembly, SPC is commonly used to:

  *  Tightening torque
  *  Gap surface difference
  *  Assembly dimensions

Combined with CPK/PPK capability analysis, it can:

  *  Determine whether the process has long-term stable supply capabilities
  *  Support mass production release (PPAP) for new projects
  *  Provide quantitative basis for continuous improvement

5. Supplier Quality Management (SQM)

In the automotive industry, SPC has long since extended from the shop floor to the supply chain:

 *  Requires suppliers to submit control charts and capability indices

 *  Remotely monitors quality trends of key components

 *  Anomalous data triggers early warnings and a closed-loop rectification process.

This has significant value for the following three points:

  *  Reducing incoming material inspection costs

  *  Preventing defective materials from entering the factory

  *  Improving the overall quality level of the supply chain

III. Core Value of SPC for Automotive Companies

1. Shifting from "Inspection Quality" to "Manufacturing Quality"

  *  Proactive problem detection

  *  Reducing rework

2. Replacing experience-based judgment with data

  *  Anomalies are supported by evidence

  *  Improvements are quantifiable

3. Supporting Systems and Audit Requirements

   *  IATF 16949

  *  VDA 6.3

  *  OEM Process Audit: The audit focuses on six key areas; the audit results directly impact business:

     —  Man: Are operators properly trained? Are key personnel certified? Are personnel changes controlled?

     —  Machine: Are key equipment identified? Is equipment status stable? Are equipment inspections and maintenance in place?

     —  Material: Are incoming materials controlled? Is batch and traceability clear? Are non-conforming materials effectively isolated?

     —  Method: Are the work instructions the latest version? Are actual operations consistent? Are error-proofing measures effective?

     —  Measurement: Are the testing equipment calibrated? Are the testing methods reliable? Is SPC used for process monitoring? (Key point)

     —  Environment: Are temperature and humidity controlled? Does cleanliness meet requirements? Do environmental changes affect quality?

4. Cost Reduction and Efficiency Improvement

  *  Reduce scrap rate

  *  Reduce downtime risk

  *  Improve delivery stability

IV. Common Challenges in Implementing SPC in the Automotive Industry

  *  Data collection relies on manual methods, resulting in insufficient timeliness.

  *  Control charts are drawn but not used, lacking closed-loop management.

  *  Non-normal data leads to CPK distortion.

  *  SPC software functions are disconnected from on-site operations.

Solutions:

  *  Promote automated data collection and systematic SPC.

  *  Establish a closed-loop mechanism of "alarm-analysis-rectification-verification".

  *  Introduce non-normal capability analysis and data transformation methods.

  *  Integrate SPC into daily production management, not just for auditing.

V. Conclusion: SPC is the "early warning radar" for automotive quality.

In the automotive industry, the cost of quality problems is often exponentially amplified. SPC is not just a control chart, but a data-driven process management philosophy.

Whoever can detect fluctuations earlier can eliminate risks earlier; whoever can truly utilize SPC can maintain stability and reliability in fierce competition.

SPC is not just a quality tool, but also a long-term competitive advantage for automotive companies.

In the field of quality management, traditional Statistical Process Control (SPC) often faces the dual challenges of "data silos" and "analysis lag." With the deepening of industrial digitalization, we believe that SPC should not be merely a drawing tool, but rather a real-time pulse connecting the production site and management decisions.

1. Real-time: Bridging the time lag between data and analysis

The system adopts a B/S architecture, achieving seamless integration from data generation to chart feedback. Through integrated HTTP, MQTT, TCP, OPC, and other interface protocols, data from sensors or detection equipment on the production line can be synchronized to the system in real time. This mechanism ensures that control charts are updated automatically without manual refresh when the page is open, truly transforming quality control from "post-event statistics" to "process prevention."

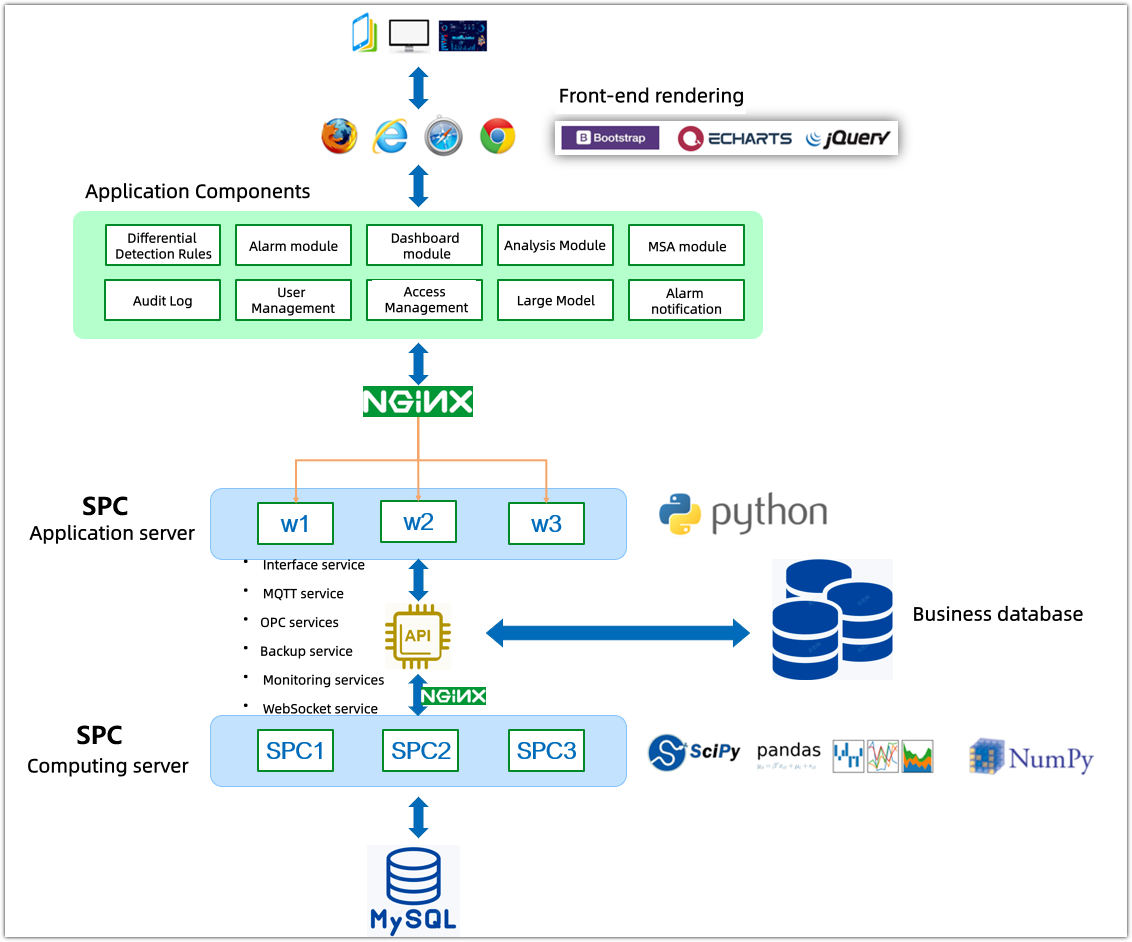
2. Multi-dimensional dashboards: Building a comprehensive monitoring view

To meet the quality management needs at different levels, we have designed three types of core monitoring dashboards, supporting the creation of an unlimited number of display pages:

• Dynamic Dashboard: Designed specifically for production workstations, it is projected onto the workshop's large screen via an independent URL. Data changes in real time as it flows in from the inspection points, allowing frontline personnel to immediately grasp the stability of the process.

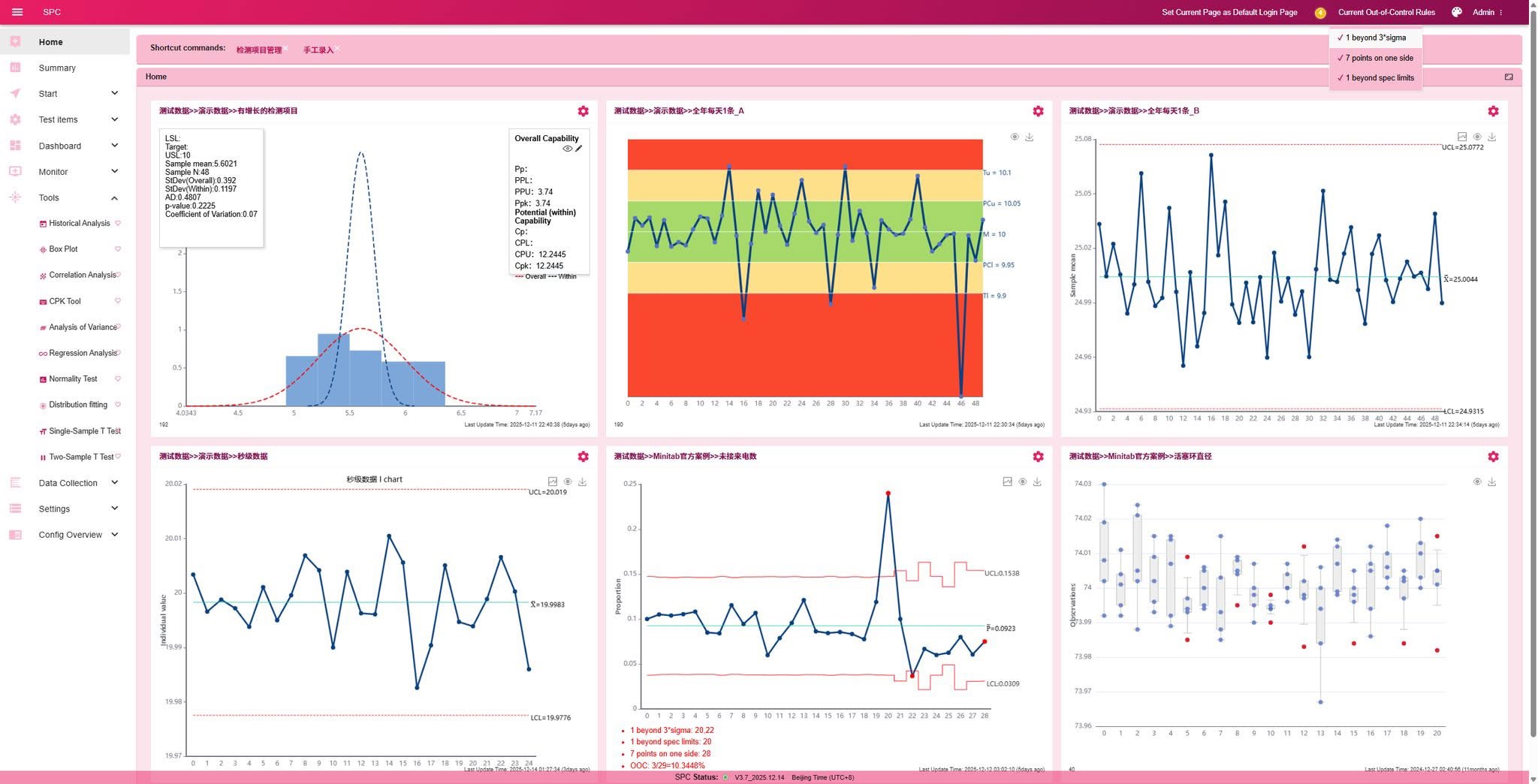
• Integrated Dashboard: Supports cross-process configuration, allowing control charts, rainbow charts, or histograms of different testing items to be freely combined in the same view, enabling centralized monitoring of complex processes.

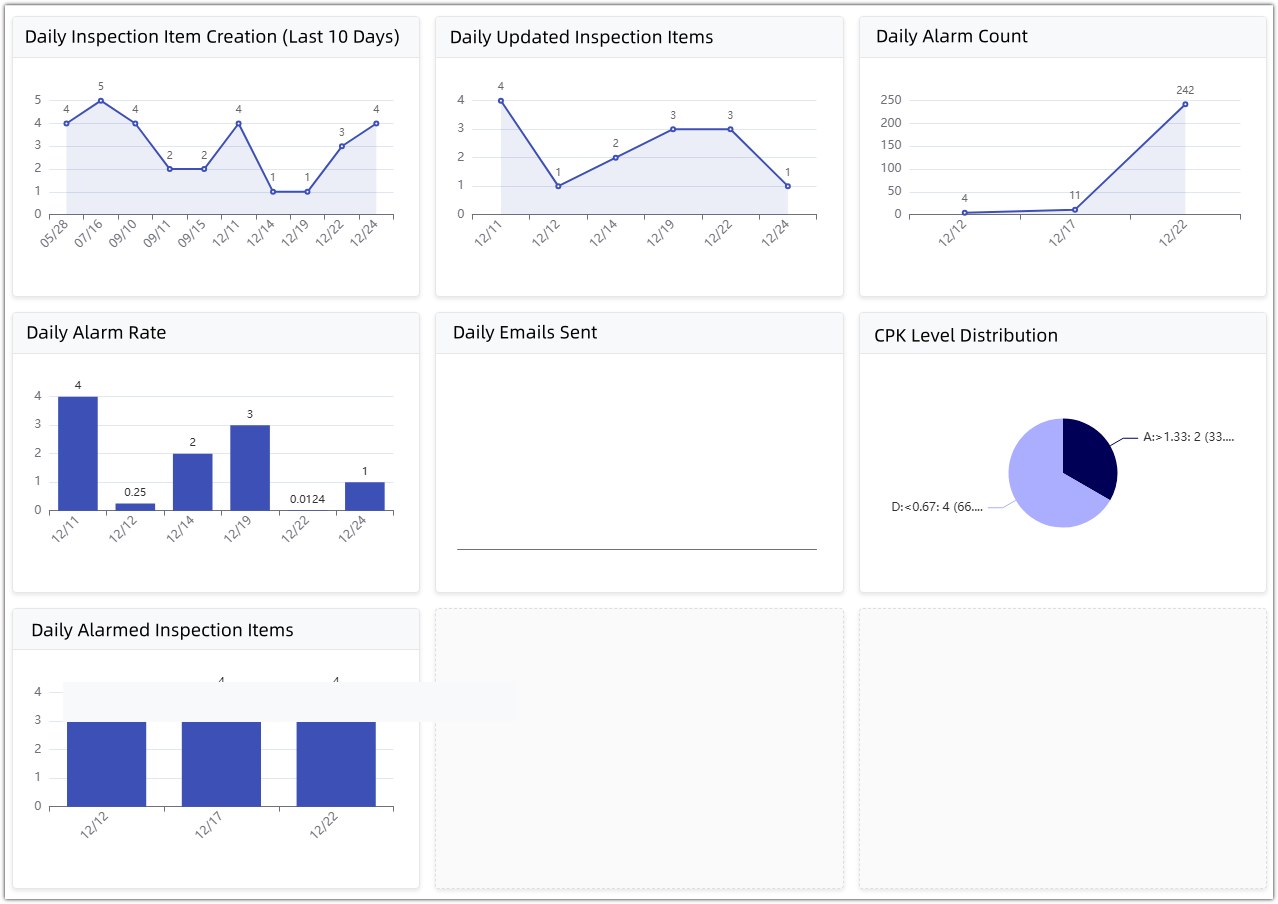
• Statistical Dashboard: Provides data summaries for management, intuitively displaying daily alarm rates, number of updated detection items, and anomaly lists, identifying systemic quality risks from a global perspective.

3. Closed-loop alarm: From anomaly detection to improvement record

A robust backend monitoring service is the core of the system's proactive defense. Its key feature lies in the independent configuration of anomaly detection rules and alerting rules:

• Omnichannel reach: The backend monitors SPC anomaly detection and CPK/PPK process capability alerts in real time. Once a rule is triggered, the system can immediately push alarm information via email, WeChat Work, DingTalk, Lark, and MQTT interface.

• Closed-loop management: Personnel receiving alarms can directly register improvement measures in the system. This closed-loop model, from anomaly detection and message push to the recording of processing results, ensures that nursing measures are traceable and that the improvement process is clear and transparent.

4. In-depth technological development: AI empowerment and reliability assurance

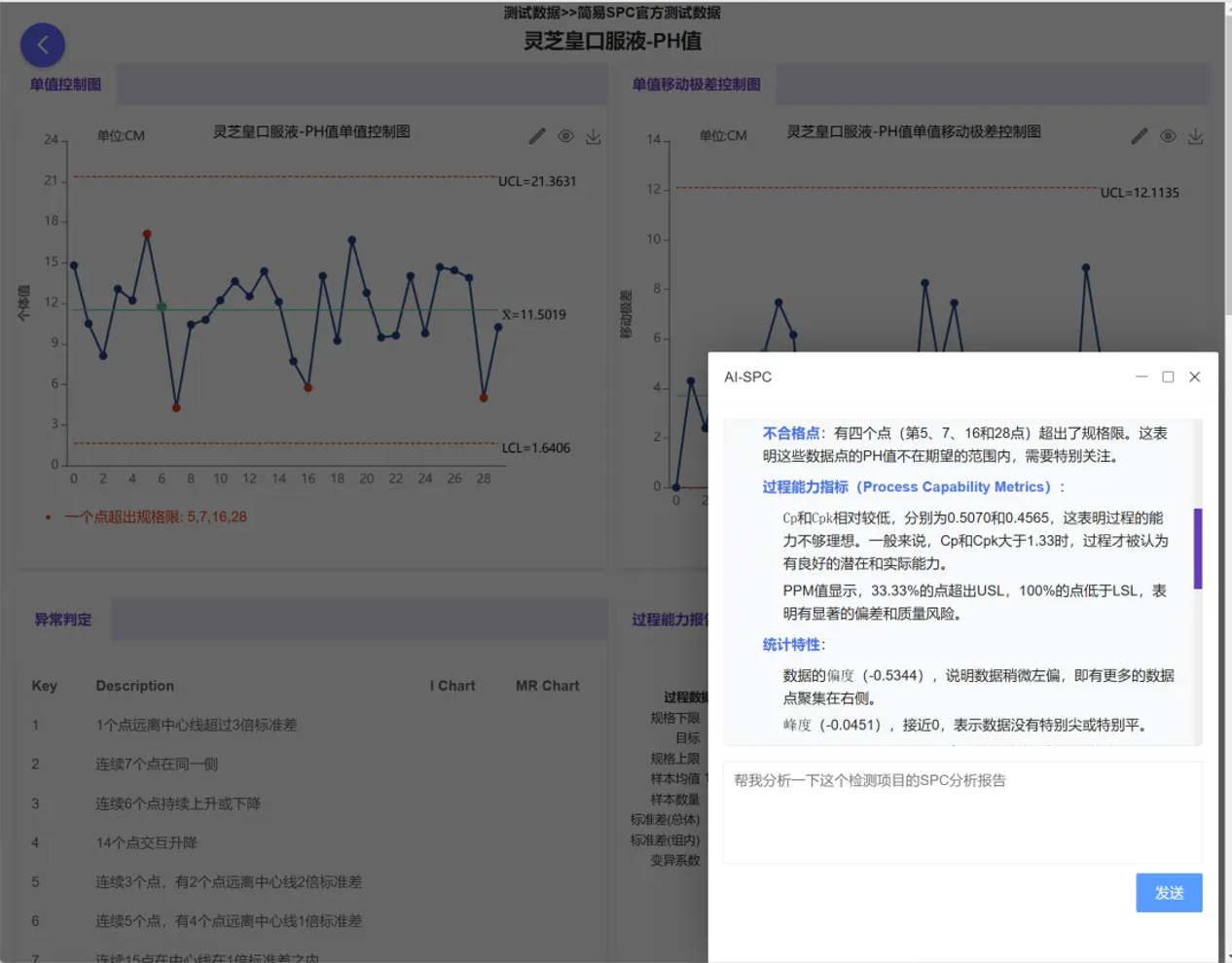
Beyond basic statistics, we've introduced more cutting-edge tools to deeply mine the value of data. The MSA (Measurement System Analysis) module covers gauge linearity and bias studies, Gage R&R studies, and more, ensuring the stability and accuracy of the gauges themselves before statistical analysis. Simultaneously, the system innovatively integrates large models such as ChatGPT and DeepSeek, enabling one-click intelligent interpretation of statistical results and assisting quality managers in quickly analyzing the causes of anomalies.

We are committed to helping enterprises build efficient digital quality systems with a lightweight architecture and extremely low technical barriers. By enabling data to "speak" and anomalies to be "detected in real time," we help China's manufacturing industry steadily move towards high-quality development.

In situations like economic downturn, poor business performance, insufficient orders, and idle production lines, besides personnel optimization and cost control, let's examine what SPC can bring to enterprises from a quality perspective.

I. Improved Performance

SPC provides objective, quantifiable process capability data, demonstrating the stability and high standards of production quality.

It enhances customer confidence, especially for customers with high quality requirements (such as those in the automotive, auto parts, and electronic chip industries).

SPC is the "key" to entering high-end supply chains. Without implementing SPC, companies may not even be eligible to bid. Furthermore, customers tend to choose suppliers with stable processes because it saves them on inspection and management costs.

It reduces customer audit risks. A mature SPC implementation system leaves a professional and reliable impression on auditors. Successfully passing audits reduces the risk of customers demanding corrective action or even canceling orders.

Compared to companies that don't implement SPC, they are more likely to obtain better audit scores and higher order quotas. It also fosters long-term partnerships, making customers less inclined to switch suppliers easily.

II. Cost Control

1. Reduce Scrap and Rework

Implementing SPC allows for real-time monitoring via control charts, with immediate alerts for any anomalies, minimizing the generation of batches of non-conforming products. This directly reduces raw material waste, labor waste, and the cost of handling scrap, while improving the first-pass yield.

2. Optimize Process Parameters

By analyzing control charts and process capability indices, key variables affecting quality can be identified, thereby determining optimal production conditions. This reduces quality problems caused by parameter fluctuations, resulting in more stable and efficient production.

3. Reduce Inspection Costs

When the process is under statistical control, the need for full inspection of the final product can be reduced, replaced by more economical sampling inspection. This saves significant investment in manpower and inspection equipment.

III. Improve Human Resource Utilization

1. Fully Utilize Idle Manpower

When orders decrease, the "waiting time" for operators, technicians, or quality personnel increases. Sometimes, large-scale workforce optimization isn't feasible. Implementing SPC allows idle staff to learn SPC theory and participate in quality analysis and improvement processes, avoiding wasted human resources. This ensures employees can still create value for the company even with insufficient working hours, preparing for future order peaks.

2. Enhancing Employee Skills

 SPC requires employees to learn statistical thinking, data collection, and problem-solving. Cultivating a core group of talent with data analysis and continuous improvement skills is an invaluable competitive advantage after economic recovery.

IV. Laying the Foundation for Long-Term Development

SPC provides objective data for problem analysis, rather than relying on experience or guesswork. This ensures management's improvement decisions are based on facts and data.

SPC can drive a shift in thinking from "producing products" to "producing qualified and stable products," cultivating a quality-conscious mindset across all employees. It improves the overall management level of the enterprise, laying the foundation for future automation and digital transformation.

Building competitive barriers, especially during economic downturns when competitors may choose to reduce quality management investment. Implementing SPC at this time often results in higher cost-effectiveness and more stable quality, seizing market share. This creates a unique competitive advantage, preparing for rapid growth after economic recovery.